LABAPPARA Materials Required
- A long cylindrical glass jar
- Transparent viscous fluid
- Metre scale
- Spherical ball
- Screw gauge
- Vernier calipers
- Stop clock
- Thread
Real Lab Procedure
- Find the least count and zero correction of the given screw guage.
- Find the diameter (d) of the ball using the screw gauge. Now, the radius(r) of ball can be calculated as ; r = d/2
- Clean the glass jar and fill it with the viscous fluid.
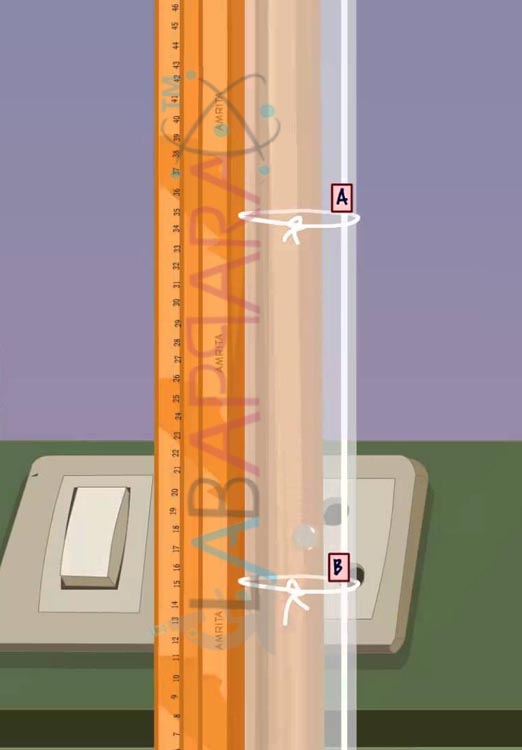
- Place a meter scale vertically beside the jar.
- Measure the inner diameter of the jar using a vernier calipers. Hence the inner radius of the jar R can be found.
- Mark two reference points A and B on the jar using two threads. The marking A is made well below the free surface of liquid, so that by the time when the ball reaches A, it would have acquired terminal velocity v.
- Adjust the position the thread B so that the distance between A and B is 60cm.
- The ball of known diameter is dropped gently in the liquid. It falls down in the liquid with accelerated velocity for about one-third of the height. Then it falls with uniform terminal velocity.
- When the ball crosses the point A, start the stop watch and the time taken by the ball to reach the point B is noted.
- If the distance moved by the ball is d and the time taken to travel is t, then velocity,
- Calculate the terminal velocity of the ball, v using the relation,
- Now, the coefficient of viscosity of the liquid can be calculated by using the formula,
- Now, repeat the experiment by changing the diameter of the ball. Calculate the value of r2/ v in each time.
- Plot a graph with r2 along X axis and terminal velocity along Y axis. We can calculate the coefficient of viscosity of the liquid by using the slope of the graph.
Procedure
- Select the environment to perform the experiment from the ‘Select the Environment’ drop down list.
- Select the liquid for which the coefficient of viscosity is to be measured, from the ‘Select Viscous Liquid’ drop down list.
- Use the ‘Select jar diameter’ slider to change the diameter of the glass jar.
- Use the ‘Select ball diameter’ slider to change the diameter of the glass ball.
- Change the distance between A and B by dragging the corresponding arrows.
- Drag the glass ball towards the jar and drop it into the liquid in the jar.
- The stop watch runs automatically as the ball reaches the point A, and stops as it leaves the point B.
- The time shown in the stop watch is noted.
- Now, calculations are done as per the observation column and the coefficient of viscosity of the selected liquid can be found out.
- Enable the ‘Show result’ checkbox to view the coefficient of viscosity of the selected liquid.
- Click on the ‘Reset’ button to redo the experiment.
Observations
To find the inner diameter of the glass jar using vernier callipers:
Value of one main scale division = ……mm
Number of divisions on the vernier = …….
Least count (L.C.) = …….. mm
= ……… cm
| Sl.No. |
M.S.R. (cm) |
V.S.R. (div.) |
V.S.R. ×L.C. (cm) |
Total reading = M.S.R.+V.S.R.×L.C. (cm) |
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
Mean diameter of the glass jar, D = ………….. cm
To find the diameter of the sphere using screw gauge:
Pitch of the screw gauge = ………. mm
Number of divisions on the circular scale = ………..
Least count of the screw gauge (L.C.) =………… mm
Zero correction of the screw gauge (z) = ………. mm
| Glass spshere No. |
P.S.R. (mm) |
Observed H.S.R. (a) (div.) |
Corrected H.S.R. (a+z) (div) |
Corrected H.S.R.×L.C. (mm) |
Total reading = P.S.R.+(Corrected H.S.R.×L.C.) (d) (mm) |
Radius of the glass ball, r=d/2 (×10-3 m) |
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
To find the terminal velocity of the sphere :
Density of the liquid, ρ = ………..kg/m3
Density of the sphere, σ = ……….kg/m3
Distance travelled by the sphere, s = ………. 10-2 m
| Glass sphere No. |
Radius of glass sphere, r (×10-3 m) |
Time taken to travel the distance s, t (s) |
Velocity, v’ = s/t (m/s) |
Terminal velocity, v = v’ [1+(2.4r/R)] (m/s)
|
r2/ v (m s) |
| 1 |
|
|
|
|
|
| 2 |
|
|
|
|
|
| 3 |
|
|
|
|
|
| 4 |
|
|
|
|
|
| 5 |
|
|
|
|
|
Calculations
Radius of the sphere, r = d/2
=………. mm
= ………×10-3 m
Inner radius of the glass jar, R = D/2
=……….. cm
=……….. ×10-2 m
Coefficient of viscosity,
= …………. Nsm-2
Square of radius versus Terminal velocity Graph :
Slope of the graph,
Coefficient of viscosity,
= …………… Nsm-2
Result
The coefficient of viscosity of the given liquid, η
By calculation, = ……………..Nsm-2
From graph, = ……………..Nsm-2








Reviews
There are no reviews yet.